L'an dernier à l'aide des infos recupérées sur le site j'ai réalisé un petit exposé en autre sur l'equilibrage du vilebrequin c'est une petite synthèse que j'ai fait (Merci Marc-R galet)
Y a peut être des trucs à ameliorer n'hésitez pas. Y a pas moyen d'avoir des vilo foireux ça coute trop cher
a Conception et équilibrage du vilebrequin
Une des clés principale du bon fonctionnement d’un moteur est l’équilibrage du vilebrequin. C’est quelque chose de relativement complexe.
Tout d’ abord il faut savoir qu’il est impossible d’équilibrer correctement un vilebrequin de monocylindre sans plusieurs balanciers d’équilibrage. (Masses entraînées en rotation dans le sens inverse du vilebrequin se situant sur des arbres. ces arbres étant entraînés à l’aide d’engrenages.) Sur le moteur d’un solex on n’utilise pas de balanciers d’équilibrage il faudra don faire des compromis.
Pour avoir une bonne approximation on décompose le problème en 2 parties les masses en rotations et les masses en translations.
Les masses en rotations sont donc constituées de : la masse, le maneton, la cage à aiguilles et une partie de la bielle. Pour déterminer la partie de la bielle à prendre en compte pour les masses en rotation on fait le montage suivant :
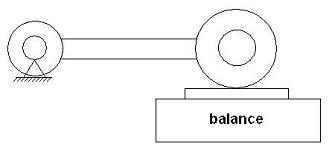
L’équilibrage des masses en rotation est facilement réalisable. On considère un système équivalent avec la masse, le maneton, la cage à aiguilles et une masse concentrée sur le maneton correspondant à la masse de la partie de la bielle en rotation mesurée précédemment. On cherche le centre de gravité de l’ensemble. En notant R1 la distance entre le centre d’inertie et l’axe de rotation du vilebrequin. On pose Mrot la masse de l’ensemble en rotation. Pour équilibrer les masses rotatives, il faut placer une masse m, à une distance r (en face du maneton telle que : m * r = Mrot * R1. En fait ceci revient à mettre le centre de gravité du système sur l’axe de rotation du vilebrequin. Au lieu de rajouter du balourd en face du maneton on peut retirer de la matière du côté du maneton ce qui a le même effet. Cette deuxième solution a l’avantage d’alléger le vilebrequin.
D’un autre côté on a les masses alternées (en translation). Il faut prendre en compte le reste de la masse de la bielle, le piston, l’axe du piston, la cage à aiguille, les segments et les circlips. C’est ici que les problèmes apparaissent. En théorie, on peut équilibrer parfaitement un mouvement alternatif avec une infinité de masses tournant à des vitesses multiples du régime moteur. Dans la pratique c’est très difficile à mettre en place. Heureusement, les efforts engendrés diminuent très rapidement, et on utilise rarement plus d’un arbre d’équilibrage. Mais c’est quand même compliqué à mettre en place car il faut un arbre qui tourne à la même vitesse que le moteur et en sens inverse. Il faut donc utiliser des engrenages.
Cependant la plus part des moteurs n’utilisent pas d’arbre d’équilibrage. On utilise juste un balourd supplémentaire, de valeur m1, à une distance r1, du côté opposé au maneton tel que : m1*r1=k*Malt*R2 Avec Malt qui correspond à la somme des masses alternatives, R2 la distance de l’axe du maneton à l’axe du vilebrequin et k un coefficient à adapter.
On peut imaginer ce qui se passe pour les valeurs extrêmes de k
k=1 correspond à un cas où on compensera totalement les efforts d’inertie au PMB et au PMB. On s’intéresse au PMB et au PMH pour les masses alternés car c’est dans ces postions qu’on a une accélération maximale. On équilibre donc totalement les inerties suivant l’axe rouge (fig1). En effet l’effort bleu est l’opposé de l’effort rouge au PMB et au PMH, ils s’annulent.
Cependant on a un balourd très important qui crée un effort maximal dans les positions intermédiaires correspondant aux vitesses maximales.
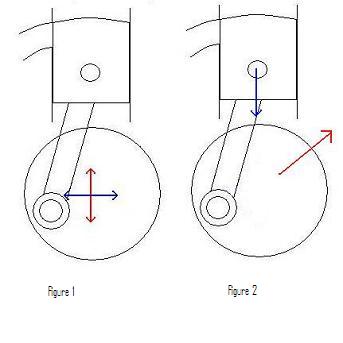
Figure 3 représentation des efforts s’appliquant sur le vilebrequin pour les 4 positions critiques
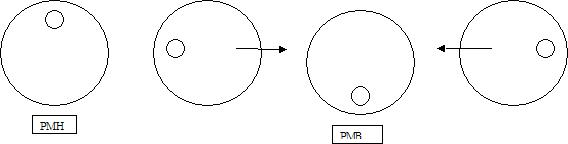
k=0 correspondrait au cas inverse on équilibrerait totalement suivant l’axe bleu. On aurait le centre d’inertie sur l’axe de rotation du vilebrequin. Cependant on aura des efforts importants qui seront crée au point mort haut et au point mort bas. Pour le cas k=0, l’effort en rouge de la figure du au balourd est inexistant.
Figure 4 représentation des efforts s’appliquant sur le vilebrequin pour les 4 positions critiques
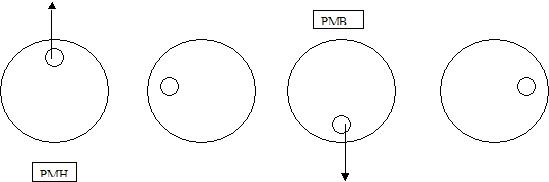
Le cas k=0.5 permet d’avoir des efforts modérés suivant l’axe bleu et l’axe rouge. A l’aide de démonstrations empirique on peut montrer que des valeurs très proches de 0.5 permettent d’avoir un bon équilibrage.
Figure 5 représentation des efforts s’appliquant sur le vilebrequin pour les 4 positions critiques
Posté: 09 Juil 2007, 19:59
j'ai regardé le post sur l'équilibrage des vilos et j'avoue que j'ai du mal a comprendre 
